👆こちらの記事では正規行列がユニタリ対角化可能であることを確認しました.
今回はそのユニタリ対角化の別の見方を書きます.
それがスペクトル分解というものです.
ほんとにただユニタリ対角化を別の表現として見るだけなのですが,計算に用いる際にそこそこ便利な場面があるので覚えておいて損はありません.
1.スペクトル分解
\(M\)を\(n \times n\)の正規行列だとします.
\(M\)の固有値は重複も含めて\(\lambda_1, \cdots, \lambda_n\)であるとしましょう.
このときあるユニタリ行列があって\[U^* M U = \text{diag}(\lambda_1, \cdots, \lambda_n)\]と表すことができます.
標準基底を\(e_1, \cdots, e_n\)とすると列ベクトル表示で
\[\text{diag}(\lambda_1, \cdots, \lambda_n) = (\lambda_1 e_1, \cdots,\lambda_n e_n) \]
と表せますね.ここでユニタリ行列\(U\)も列ベクトル表示して
\[U = (u_1, \cdots, u_n)\]
とします.すると
\begin{align*}
M &= U \text{diag}(\lambda_1, \cdots, \lambda_n) U^*\\
&= (u_1, \cdots, u_n) (\lambda_1 e_1, \cdots,\lambda_n e_n) \begin{pmatrix}
u_1^* \\ \vdots \\ u_n^*
\end{pmatrix}\\
&= (\lambda_1 u_1, \cdots,\lambda_n u_n) \begin{pmatrix}
u_1^* \\ \vdots \\ u_n^*
\end{pmatrix}\\
&= \lambda_1 u_1 u_1^* + \cdots + \lambda_n u_n u_n^*
\end{align*}
というように固有値とその固有ベクトルから求まる\(\lambda_i u_i u_i^*\)という形の行列の和として表すことができました.これをスペクトル分解といいます.
\(M\)のスペクトル分解とは
\[M = \sum_{i=1}^n \lambda_i u_i u_i^*\]
見た目からして分解になってますが,分解の意味をはっきりさせておきましょう.
2.なにが分解なのか
固有値に重複があるかもしれないので,番号をふっておきます.
固有値\(\lambda_i\)に対して対応する固有ベクトルは\(m\)本あって\[u_{i_1}, \cdots, u_{i_m}\]とします.
このように定めるとスペクトル分解の内,固有値\(\lambda_i\)に対応するのは,
\[\lambda_i \sum_{k = 1}^{m} u_{i_k} u_{i_k}^*\]
となります.この行列を\[P_i = \sum_{k = 1}^{m} u_{i_k} u_{i_k}^*\]とおいて,その作用を見てみましょう.
まず\((u_1, \cdots, u_n)\)はユニタリ行列なので正規直交基底になっています.つまり正規化されていて,なおかつ複素ベクトルに対する内積\[\langle x, y\rangle := y^* x\]について,
\[\langle u_i, u_j\rangle = \delta_{ij}\]
を満たします.
そこで任意のベクトル\(v \in \mathbb{C}^n\)は\[v = \sum_{i = 1}^n c_i u_i\]と展開することができます.すると,
\begin{align*}
P_i v &= \sum_{k = 1}^{m} u_{i_k} u_{i_k}^* \sum_{j = 1}^n c_j u_j\\
&= \sum_{k = 1}^{m} \sum_{j = 1}^n c_j u_{i_k} \langle u_j, u_{i_k}\rangle \\
&= \sum_{k = 1}^{m} \sum_{j = 1}^n c_j u_{i_k} \delta_{j\ i_k} \\
&= \sum_{k = 1}^{m} c_{i_k} u_{i_k}
\end{align*}
となります.これを見ると元のベクトルから\(u_{i_1}, \cdots, u_{i_m}\)の成分のみ抽出した形になってます.つまり固有値\(\lambda_i\)に対応する固有空間への射影になっていますね.
ということで,固有値が重複を除いて,異なるものが\(N\)種類あるとしましょう.\(N \leq n\)です.このとき射影行列\(P_i\ (i = 1, \cdots, N)\)は\(\lambda_i\)に対応する固有空間を張る固有ベクトルの本数を\(m_i\)として,各固有空間に対し\[P_i = \sum_{k = 1}^{m_i} u_{i_k} u_{i_k}^*\]と定義できます.
これを用いてスペクトル分解は\[M = \sum_{i = 1}^N \lambda_i P_i\]と書き直せます.つまり分解というのは固有空間へ分解しているということだったわけですね.
ただし,ただの固有空間への分解ではないんですね.
3.もっというと直交分解
射影行列\(P_i = \sum_{k = 1}^{m} u_{i_k} u_{i_k}^*\)の性質をもう少し調べていきます.
固有ベクトルの本数は\(i\)に依存しているのでほんとは\(m\)ではなく\(m_i\)と書いた方が丁寧ですが,若干見た目が煩雑なので\(m\)本と書くことにさせてください.
固有値\(\lambda_i\)に対応する固有空間を\(V_i\)とおきます.\(V_i = \text{span}(u_{i_1}, \cdots, u_{i_{m}})\)です.
\begin{align*}
1.\quad &P_i^* = P_i\\
2.\quad &x \in V_i\ のとき\ P_i x = x\\
3.\quad &P_i^2 = P_i
\end{align*}
示してみます.
1.については明らかですね.\(P_i^* = \sum_{k = 1}^{m} (u_{i_k} u_{i_k}^*)^* = P_i\)です.
2.についてはほとんど先ほどの射影の議論と同じです.\(x \in V_i\)ということなので,\[x = \sum_{k = 1}^m c_{i_k} u_{i_k}\]と書けますから,
\begin{align*}
P_i x &= \sum_{l = 1}^m u_{i_l} u_{i_l}^* \sum_{k = 1}^m c_{i_k} u_{i_k} \\
&= \sum_{k,l = 1}^m u_{i_l} c_{i_k} \delta_{i_l\ i_k} \\
&= \sum_{k = 1}^m u_{i_k} c_{i_k} \\
&= x
\end{align*}
3.については2.から従います.つまり任意のベクトル\(x \in \mathbb{C}^n\)に対して\(P_i x \in V_i \)ですから\(P_i^2 x = P_i (P_i x) = P_i x \)ということです.
さてでは\(P_i\)がただの射影ではなく直交射影であることを確認しましょう.\(P_i\)は元のベクトルの\(V_i\)に属する成分を伸ばしたり縮めたりせずそのまま射影できるんですね.
こんなイメージです.
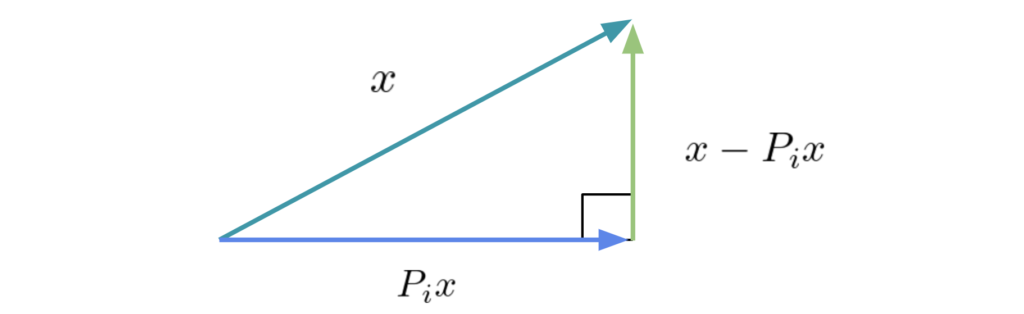
ということで\(P_i x\)と\(x – P_i x\)が直交していることを確かめていきましょう.
\begin{align*}
\langle P_i x, x -P_i x \rangle &= (x -P_i x)^* \underset{1.を使う!}{\underline{P_i}} x\\
&= (x -P_i x)^* P_i^* x\\
&= (P_i x -\underset{3.を使う!}{\underline{P_i^2}} x)^* x\\
&= (P_i x -P_i x)^* x \\
&= 0
\end{align*}
ということで\(P_i\)が直交射影であることまでわかりました.
正規行列は固有空間への直交射影に分解できる

最後まで読んでくださいましてありがとうございました


コメント