高校の物理で習った等速円運動の方程式って \( m \frac{v^2}{r} = F \) って形でしたよね
この \( \frac{v^2}{r}\) って何だろうって思いませんでしたか?
もちろん加速度なんですが、どうにもこれが加速度には見えづらいですよね
今回はこれを解決いたします
1.直交座標と極座標の単位ベクトル
まず加速度や速度を考える前に座標を取らねばなりません
というのも速度は座標の微小時間当たりの変化の割合ですし、加速度は速度の微小時間当たりの変化の割合だからです、根っこの部分は座標なんですね
では座標を取るには何が必要かというと、ご存じ「単位ベクトル」です
例えば最も馴染みのある \(xy\) 座標の単位ベクトルは
\(\vec{\mathstrut e_x} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \) \(\vec{\mathstrut e_y} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \)
ですね
この二つのベクトルをそれぞれ定数倍して和をとることで、平面上のすべての点を表せるってわけです
例えば点 \((2, 3)\) を表したければ
\(2 \vec{\mathstrut e_x} + 3 \vec{\mathstrut e_y} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} \)
ってな感じです
では極座標の単位ベクトルを考えてみましょう、図形的な対応から \(xy\) 座標の単位ベクトルを用いて極座標の単位ベクトルを表したいです
まず \(xy\) 座標の単位ベクトルは下図のオレンジ色です
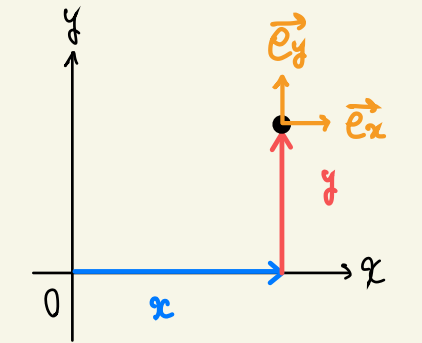
単位ベクトルはさきほど実際のベクトルを見たように \(x\) 軸と \(y\) 軸それぞれに平行です
つまり座標として \(x\) が増える方向に \(\vec{\mathstrut e_x}\) が向いていて、 \(y\) が増える方向に \(\vec{\mathstrut e_y}\) が向いています
次に \(r\theta\) 座標、すなわち極座標の単位ベクトルは下図の緑色です
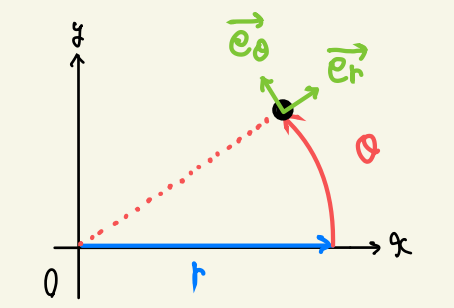
\(xy\) 座標も同時に図示してみました
極座標の単位ベクトルは \(\theta\) に依存しているので注意が必要です
というのも \(xy\) 座標と同じく \(r\) が増える方向に \(\vec{\mathstrut e_r}\) が向いていて、 \(\theta\) が増える方向に \(\vec{\mathstrut e_\theta}\) が向いていなければならないからです
\(\vec{\mathstrut e_r}\) は常に極( \(xy\) 座標における原点)から遠ざかる方向に向いていて、\(\vec{\mathstrut e_\theta}\) は \(\theta\) が増える方向、つまり \(\vec{\mathstrut e_r}\) に直交する方に向いていなけらばならないですね
よって非常に大事なことなのですが \(\vec{\mathstrut e_r}\) と \(\vec{\mathstrut e_\theta}\) は注目している点の \(\theta\) によって変化するので
動く質点を考える時は \(\vec{\mathstrut e_r}\) と \(\vec{\mathstrut e_\theta}\) が時々刻々と変化していきます
というのも動く質点は常に \(r\) 方向にのみ運動する特殊ケースを除いて、 \(\theta\) が時間変化するからです
後で単位ベクトルを時間微分することになるのですが \(\vec{\mathstrut e_r}\) と \(\vec{\mathstrut e_\theta}\) は時間変化します、 \(\vec{\mathstrut e_x}\) と \(\vec{\mathstrut e_y}\) は時間によらず一定です、というのも \(\vec{\mathstrut e_x}\) と \(\vec{\mathstrut e_y}\) は注目する点によらず常に同じベクトルだからですね
続いて今考えた\(\vec{\mathstrut e_x}\) と \(\vec{\mathstrut e_y}\) と \(\vec{\mathstrut e_r}\) と \(\vec{\mathstrut e_\theta}\) の関係を調べます
単位ベクトルは大きさが1になるように作ってますからオレンジのベクトルと緑のベクトルを同一円周上に図示すると
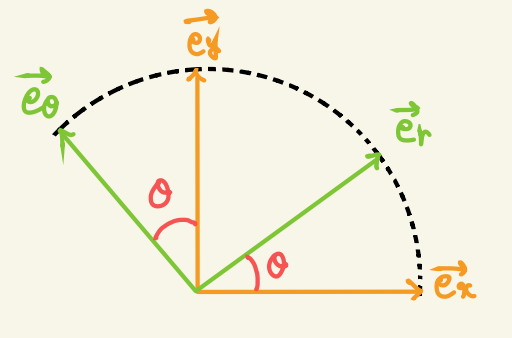
よって \(\vec{\mathstrut e_r}\) 方向と \(\vec{\mathstrut e_\theta}\) 方向に \(\vec{\mathstrut e_x}\) と \(\vec{\mathstrut e_y}\) を分解すると
\(\vec{\mathstrut e_r} = \vec{\mathstrut e_x}\cos\theta + \vec{\mathstrut e_y}\sin\theta\)
\(\vec{\mathstrut e_\theta} = -\vec{\mathstrut e_x}\sin\theta + \vec{\mathstrut e_y}\cos\theta \)
となります
2.極座標を微分していく
ここから極座標における速度、加速度を求めていきます
今注目する質点の位置ベクトルを \(\vec{\mathstrut r}\) とします
質点が動く状況を考えるので \(\vec{\mathstrut r}=\vec{\mathstrut r}(t)\) であることを意識します
質点の極座標が \((r, \theta)\) として、この \(\vec{\mathstrut r}\) を極座標の単位ベクトルを用いて表すと
\(\vec{\mathstrut r} = r \vec{\mathstrut e_r}\)
となります、\(\vec{\mathstrut e_r} \) が原点から質点の方向を向いていて、原点から質点までの距離が \(r\) なのでこう表せるわけです
さて速度は位置の時間微分、加速度は速度の時間微分なわけですから、今得た式をどんどん微分していきます
ですがその前に計算をスムーズに行うため下準備をしておきます
先ほど得た
\(\vec{\mathstrut e_r} = \vec{\mathstrut e_x}\cos\theta + \vec{\mathstrut e_y}\sin\theta\)
\(\vec{\mathstrut e_\theta} = -\vec{\mathstrut e_x}\sin\theta + \vec{\mathstrut e_y}\cos\theta \)
の時間微分を考えます、すると \(\vec{\mathstrut e_x}\) と \(\vec{\mathstrut e_y}\) は時間によらず一定なので
\(\begin{eqnarray} \dfrac{d}{dt} \vec{\mathstrut e_r} &=& -\vec{\mathstrut e_x}\dfrac{d\theta}{dt}\sin\theta + \vec{\mathstrut e_y}\dfrac{d\theta}{dt}\cos\theta \\ &=& \dfrac{d\theta}{dt} \vec{\mathstrut e_\theta} \end{eqnarray}\)
\(\begin{eqnarray} \dfrac{d}{dt} \vec{\mathstrut e_\theta} &=& -\vec{\mathstrut e_x}\dfrac{d\theta}{dt}\cos\theta \: -\: \vec{\mathstrut e_y}\dfrac{d\theta}{dt}\sin\theta \\ &=& -\dfrac{d\theta}{dt} \vec{\mathstrut e_r} \end{eqnarray}\)
となり \(\vec{\mathstrut e_r}\) と \(\vec{\mathstrut e_\theta}\) の微分が \(\vec{\mathstrut e_\theta}\) と \(\vec{\mathstrut e_r}\)で表すことができました
では \(\vec{\mathstrut r} = r \vec{\mathstrut e_r}\) の時間微分を実行します、積の微分法を用います
\(\begin{eqnarray} \vec{\mathstrut v} &=& \dfrac{d}{dt} r \vec{\mathstrut e_r} \\ &=& \dfrac{dr}{dt} \vec{\mathstrut e_r} + r \dfrac{d}{dt}\vec{\mathstrut e_r} \\ &=& \dfrac{dr}{dt} \vec{\mathstrut e_r} + r \dfrac{d\theta}{dt}\vec{\mathstrut e_\theta} \end{eqnarray}\)
この式から分かることは、質点の \(r\) 方向への速度が \(\dfrac{dr}{dt}\) であり、 \(\theta\) 方向への速度が \(r\dfrac{d\theta}{dt}\) であるということです
ここで円運動と今得た式の関係を考えてみると、円運動は原点との距離が一定に保たれている運動のことですから \(r = const.\) であり \(\dfrac{dr}{dt}=0\) ですね、さらに \(\dfrac{d\theta}{dt}\) は角速度ですから、馴染みのある \(\omega = \dfrac{d\theta}{dt}\) で書くと
\(\vec{\mathstrut v} = r\omega\vec{\mathstrut e_\theta}\)
となって円運動は半径方向と直交する方向( \(\theta\)方向 )に速度 \(r\omega\) で運動するという公式を得ることができます
さて最後に加速度の微分を考えます、こちらも積の微分でゴリゴリ計算します
\(\begin{eqnarray} \vec{\mathstrut a} &=& \dfrac{d}{dt} \vec{\mathstrut v} \\ &=& \dfrac{d}{dt} \left \lbrack \dfrac{dr}{dt} \vec{\mathstrut e_r} + r \dfrac{d\theta}{dt}\vec{\mathstrut e_\theta} \right \rbrack \\ &=& \dfrac{d^2 r}{dt^2} \vec{\mathstrut e_r} + \dfrac{dr}{dt} \dfrac{d}{dt} \vec{\mathstrut e_r} + \dfrac{dr}{dt} \dfrac{d\theta}{dt} \vec{\mathstrut e_\theta} + r \dfrac{d^2 \theta}{dt^2} \vec{\mathstrut e_ \theta} + r \dfrac{d\theta}{dt}\dfrac{d}{dt}\vec{\mathstrut e_\theta} \\ &=& \dfrac{d^2 r}{dt^2} \vec{\mathstrut e_r} + \dfrac{dr}{dt}\dfrac{d\theta}{dt} \vec{\mathstrut e_\theta} + \dfrac{dr}{dt} \dfrac{d\theta}{dt} \vec{\mathstrut e_\theta} + r \dfrac{d^2 \theta}{dt^2} \vec{\mathstrut e_ \theta} \:-\: r\left( \dfrac{d\theta}{dt}\right)^2 \vec{\mathstrut e_r} \\ &=& \left\lbrack \dfrac{d^2 r}{dt^2}\:-\: r\left( \dfrac{d\theta}{dt}\right)^2 \right\rbrack\vec{\mathstrut e_r} + \left\lbrack 2\dfrac{dr}{dt}\dfrac{d\theta}{dt} + r \dfrac{d^2 \theta}{dt^2} \right\rbrack \vec{\mathstrut e_ \theta} \end{eqnarray}\)
なかなかイカツイ式ですが、これは質点が動くこととに連動して極座標の単位ベクトルの向きが変化することによります
3.等速円運動の加速度について
では今まで求めた式を用いて等速円運動の式の加速度を導きましょう
円運動なので \(r = const.\) ですから
\(\dfrac{dr}{dt} = 0, \: \dfrac{d^2 r}{dt^2}=0\)
等速なので \(v=r\omega=const.\) ですから \(r=const.\) より \(\omega = const.\) で
\(\dfrac{d\omega}{dt} = \dfrac{d^2 \theta}{dt^2} = 0\)
よって等速円運動の加速度は、先ほど得た式に代入計算して
\(\vec{\mathstrut a} = -r\omega^2\vec{\mathstrut e_r}\)
となることが分かりました
\(\vec{\mathstrut e_r}\) は原点から質点に向かうベクトルなので、マイナスがつくことで加速度が質点から原点に向かっていることを表せています
もちろん \(\omega = \dfrac{v}{r}\) ですから加速度の大きさは \(\dfrac{v^2}{r}\) となることが確認できます
4.まとめ
今回は等速円運動の運動方程式を、高校物理で習うような図形的解釈を用いた方法ではなく、数式的にアプローチすることで導きました
おそらく大学の力学の最初の授業で取り組む内容ですので式変形は少々大変ですが、非常に重要な内容だと思います

最後まで読んでくださいましてありがとうございました


コメント