力学においては運動方程式を解くことで、考えている物体の運動を解析することができました
電磁気学でも同じように、これを解けば電磁気の現象が見える!という方程式があります
それがマクスウェル方程式です
ただ、運動方程式は1つだけだったのですが、マクスウェル方程式は4つあります。
(実際はマクスウェル方程式の4つとローレンツ力の式で電磁気現象が分かるようになります)
この記事ではマクスウェル方程式の書き方の一つである積分形をリストアップし、その式のイメージを説明したいと思います。
1.マクスウェル方程式の積分形
そもそもマクスウェル方程式がどんな物理量の関係を表しているかというと
電荷密度\(\rho\)、電流密度\(\boldsymbol{j}\)、電場 \(\boldsymbol{E}\)、磁束密度 \(\boldsymbol{B}\) です
\[\int_S \boldsymbol{E} \cdot \boldsymbol{n} dS= \frac{1}{\epsilon_0} \int_V \rho dV \qquad \cdots (1)\]
\[\oint_C \boldsymbol{E} \cdot d\boldsymbol{r} = -\frac{d}{dt}\int_S \boldsymbol{B} \cdot \boldsymbol{n} dS\qquad \cdots (2)\]
\[\int_S \boldsymbol{B} \cdot \boldsymbol{n} dS =0\qquad \cdots (3)\]
\[c^2\oint_C \boldsymbol{B} \cdot d\boldsymbol{r} = \frac{d}{dt}\int_S\boldsymbol{E}\cdot\boldsymbol{n}dS + \frac{1}{\epsilon_0}\int_S \boldsymbol{j} \cdot \boldsymbol{n} dS\qquad \cdots (4)\]
以上の4つがマクスウェル方程式です
つまり電磁気の現象は \(\rho ,\boldsymbol{j}, \boldsymbol{E}, \boldsymbol{B}\) の情報に集約されるってことなんですね、とっても簡潔ですよね
見てくれはなかなかおぞましいですが、以下で一つずつイメージをつけていきたいと思います
時間変化があるかないか、考えている曲面が閉じているか閉じていないかをしっかり区別したいです
2.(1):電荷と電場の関係
まず(1)です
\[\int_S \boldsymbol{E} \cdot \boldsymbol{n} dS= \frac{1}{\epsilon_0} \int_V \rho dV \]
まず文字が何を表しているか書き上げます
- \(S\)・・・今考えている閉じた曲面
- \(\boldsymbol{E}\)・・・電場
- \(\boldsymbol{n}\)・・・閉曲面Sの単位法線ベクトル
- \(\epsilon_0\)・・・真空の誘電率
- \(V\)・・・ \(S\) によって囲まれた領域
- \(\rho\)・・・電荷密度
今リストアップした内容を図にまとめると、以下のようになります
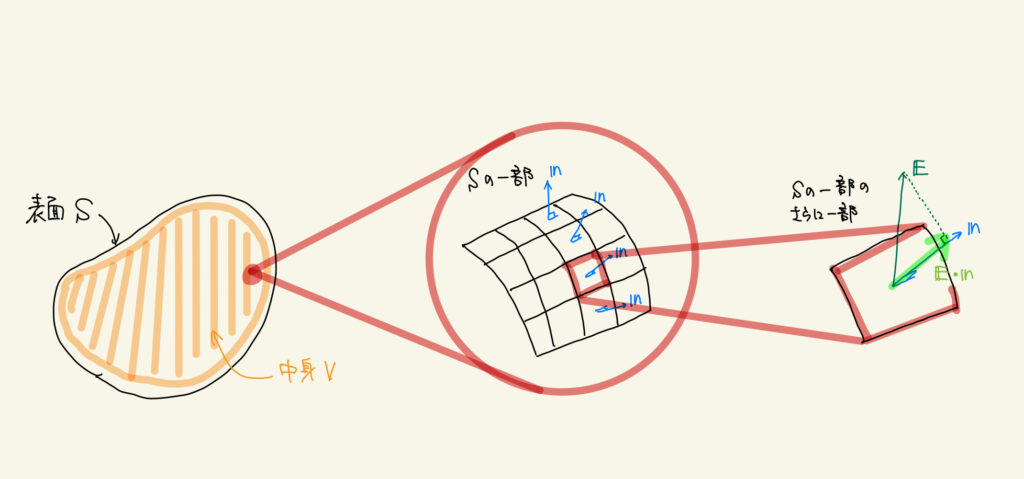
図の黄緑の矢印 \(\boldsymbol{E} \cdot \boldsymbol{n}\) は、 \(\boldsymbol{n}\) が単位法線ベクトルなので、 \(\boldsymbol{E} \cdot \boldsymbol{n}=|\boldsymbol{E}||\boldsymbol{n}|\cos\theta=|\boldsymbol{E}|\cos\theta\) と計算出来るので、電場の \(S\) に垂直な成分です
なので左辺の \(\int_S \boldsymbol{E} \cdot \boldsymbol{n}dS\) の意味は
\(S\) 表面に垂直な電場 \(\boldsymbol{E} \cdot \boldsymbol{n}\) を足しあげたもの
となり、右辺の \(\frac{1}{\epsilon_0} \int_V \rho dV\) は、 \(\rho dV = dQ\) であることから
体積\(V\) の中身の電荷\(dQ\)を足しあげたもの
ということですから、結局のところ
空間上のある領域 \(V\) から飛び出す電場は、 \(V\) の中身の電荷に比例する
という意味ですね(比例定数は \(\frac{1}{\epsilon_0}\) です)
電荷によって電場が形成されているという因果関係を意識しましょう
高校物理でもでてきたガウスの法則の本当の姿ですね
3.(2):電場と磁場の関係
次は(2)です
\[\oint_C \boldsymbol{E} \cdot d\boldsymbol{r} = -\frac{d}{dt}\int_S \boldsymbol{B} \cdot \boldsymbol{n} dS\]
これも文字の意味を見ておきましょう
- \(C\) ・・・今考えている閉曲線( \(S\) の縁の部分)
- \(\boldsymbol{E}\)・・・電場
- \(S\) ・・・今考えている曲面
- \(\boldsymbol{B}\)・・・磁束密度
- \(\boldsymbol{n}\)・・・閉曲面Sの単位法線ベクトル
という感じです、こちらも図示すると
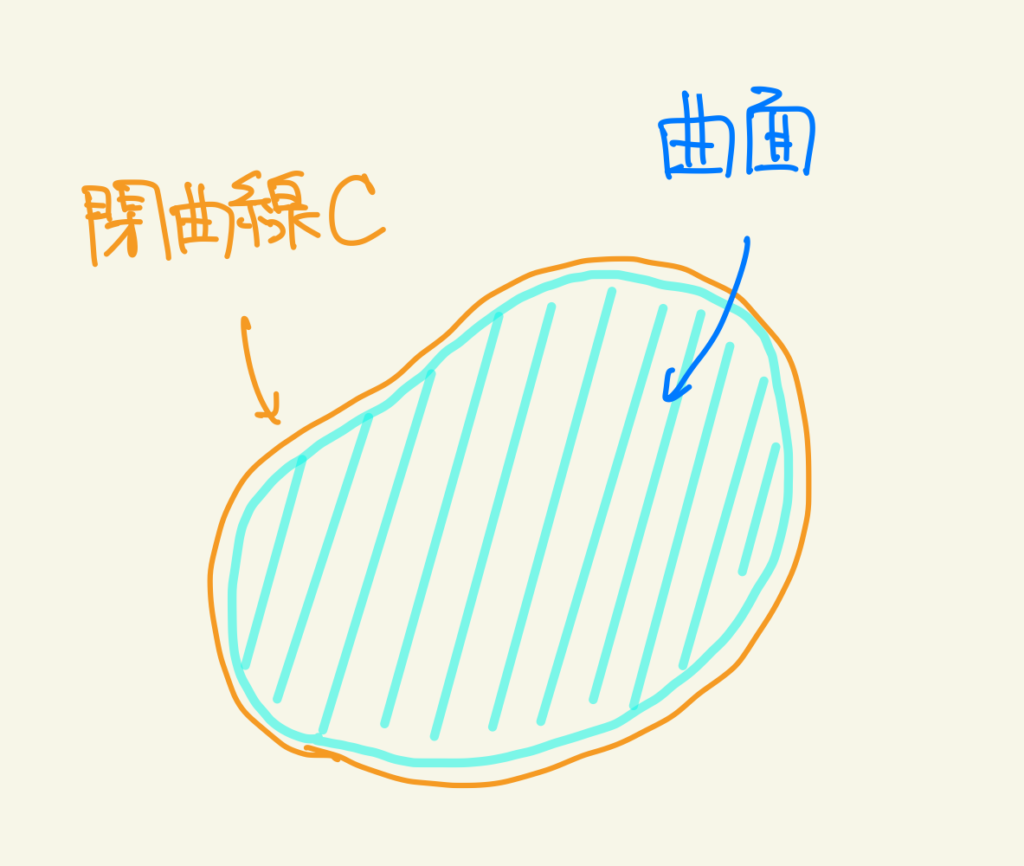
ここで注意なのは、左辺の線積分に向きがついていることです
角度の定義と同じく、z軸正の方向に右ねじが進む向きです
さてそれを踏まえて、(2)式のイメージは下の図のようになります
(2)は(1)とちがって、時間変化であることに気を付けましょう
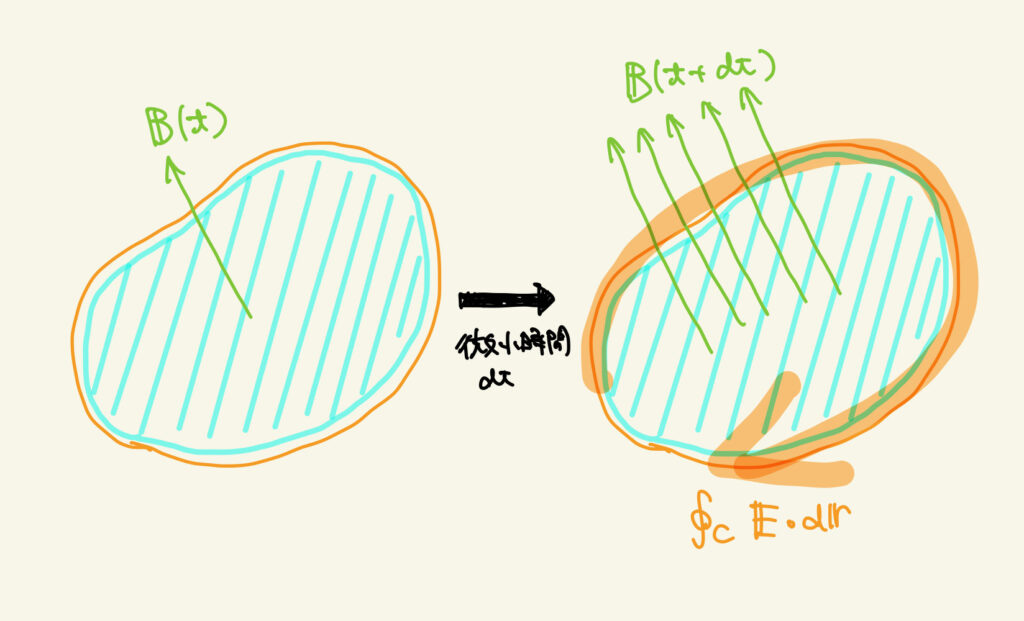
微小時間 \(dt\) の間に、磁束密度が増加(1本➡5本)したので、閉曲線 \(C\) 時計回りに電場ができます
磁場の変化を妨げる方向に電場が発生する
っていう現象ですね、ファラデーの法則です
4.(3):磁場について
\[\int_S \boldsymbol{B} \cdot \boldsymbol{n} dS =0\]
今まででてきた文字と役割は同じで
- \(S\) ・・・今考えている閉曲面
- \(\boldsymbol{B}\)・・・磁束密度
- \(\boldsymbol{n}\)・・・閉曲面Sの単位法線ベクトル
磁石をすっぽり覆う閉曲面 \(S\) をイメージしてみましょう
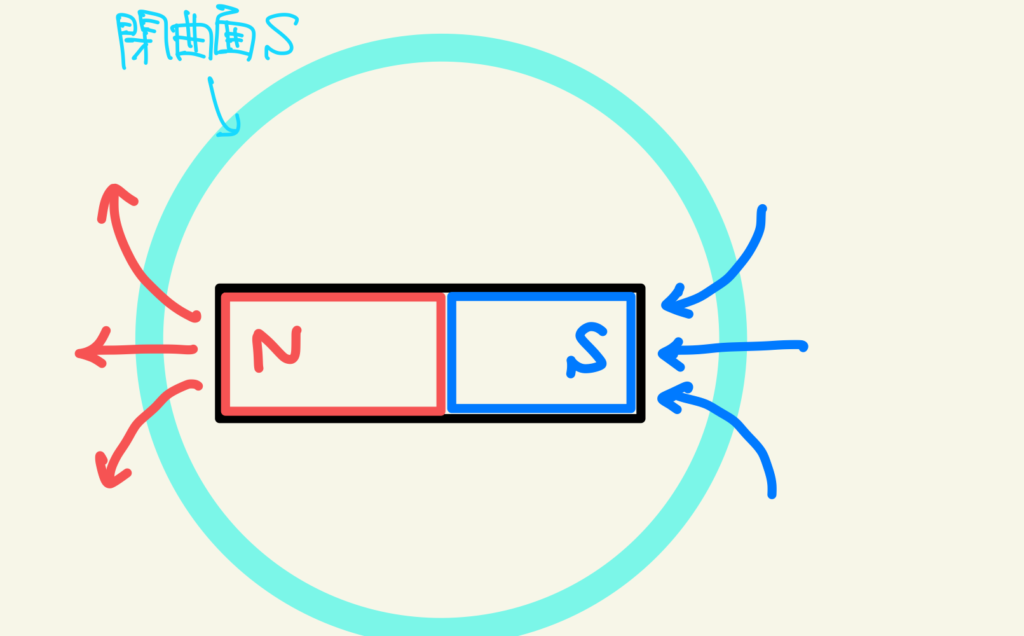
N極から出た磁束密度の矢印はぐるっと回ってS極に入っていきます
よって閉曲面 \(S\) に注目すると、磁力線の出ていく数(3本)と入って来る数(3本)は常に一致するわけです
よく見ると、この(3)式は(1)式ととってもよく似ていますよね
では違いが何かというと、もちろん右辺です
(1)式においては電荷がありますが、(3)式においてはその電荷に対応するものがありません
これ、何を言っているかというと、領域 \(S\) の中で電荷はプラスとマイナスで偏りを作れますが
領域 \(S\) の中で磁気は偏りを作れない ⇔ N極とS極は分離できない
電気には電荷という符号のある量が存在しますが、磁気にはいわゆる「磁荷」というN極だけ or S極だけという状態が存在しないということですね
モノポールが存在しないということです
5.(4):磁場と電場と電流密度の関係
\[c^2\oint_C \boldsymbol{B} \cdot d\boldsymbol{r} = \frac{d}{dt}\int_S\boldsymbol{E}\cdot\boldsymbol{n}dS + \frac{1}{\epsilon_0}\int_S \boldsymbol{j} \cdot \boldsymbol{n} dS\]
式が長いですが、登場する文字の意味は
- \(c\) ・・・光の速度
- \(C\) ・・・今考えている閉曲線( \(S\) の縁の部分)
- \(\boldsymbol{B}\)・・・磁束密度
- \(S\) ・・・今考えている曲面
- \(\boldsymbol{E}\)・・・電場
- \(\boldsymbol{n}\)・・・曲面Sの単位法線ベクトル
- \(\epsilon_0\)・・・真空の誘電率
これのイメージは右辺の二項を分割して考えていきましょう
まず右辺第一項について
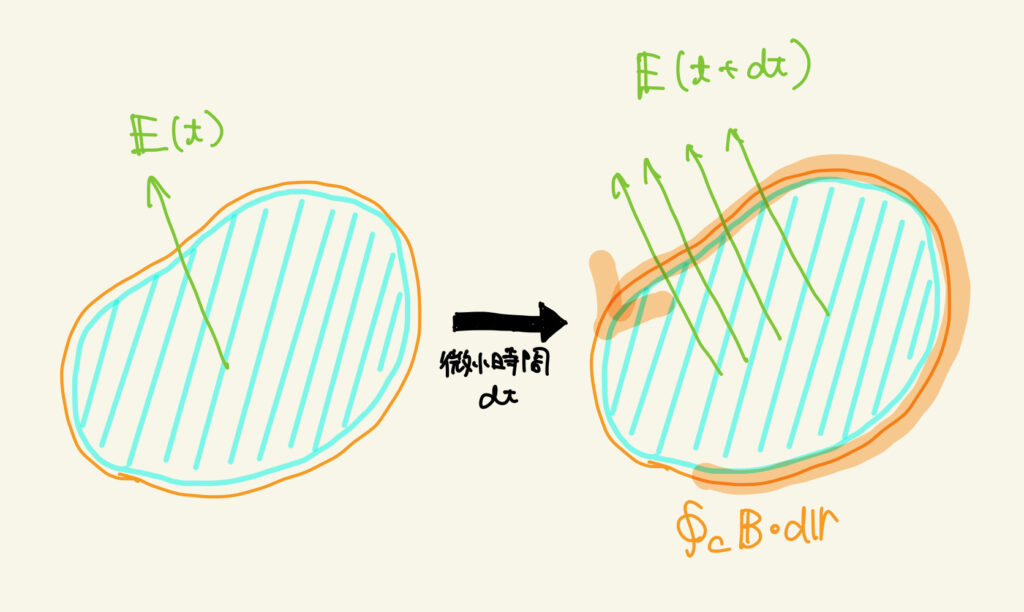
これは時間変化を伴っている現象だということに注意してください
領域 \(S\) で電場が増えると、縁のところに右ねじが進む向きに磁場ができる
ということです、右ねじの法則ですね
さて右辺第二項は
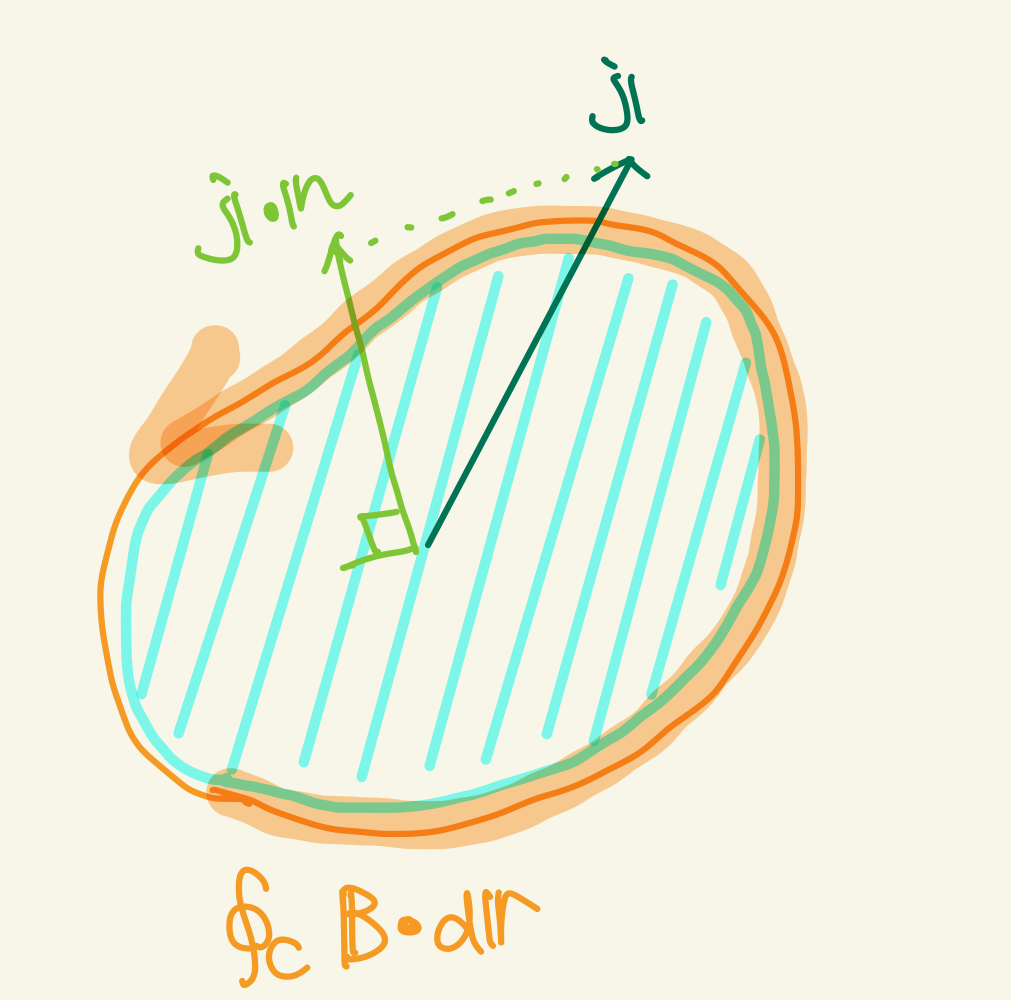
電流密度 \(\boldsymbol{j}\) を面積分すれば定義通り電流を得ますので
電流によって磁場が形成されている
という因果関係を式に書いたものなわけです
以上のように、右ねじの法則と電流によって磁場が形成されることの2つを重ね合わせの形で書き表したのが(4)式だということになります
6.まとめ
以上でマクスウェル方程式の積分形のイメージがぼんやりとできると幸いです
まとめると
(1):電荷によって電場が形成されるという因果関係
(2):磁場の変化を妨げる向きに電流が形成される
(3):N極とS極は分離できない
(4):電流によって磁場が形成される&電場の増加で右ねじの向きに磁場が形成される
という感じです、かなり雑なイメージだと思いますがマクスウェル方程式のゴツさに対して、多少恐怖心が薄れれば何よりです

最後まで読んでくださいましてありがとうございました



コメント