主値積分という複素積分のテクニックを使うことで,複素関数の実部と虚部を互いに結びつけることができます.それがKramers-Kronig(クラマースクローニッヒ)の関係式です.KK関係と略されることもあります.
この式は物理において統計力学だったり光学だったり様々な分野で登場します.
1. Kramers-Kronigの関係式
まずどんな関係式なのかというと,
Kramers-Kronigの関係式
因果的な実関数\(f(t)\)のフーリエ変換を
\[F(\omega) = \int_{-\infty}^{\infty} f(t) e^{i\omega t}dt\]
とおく.このとき\(F(\omega) = F_R(\omega) + iF_I(\omega)\)の実部と虚部が主値積分によって以下のように結びつく:
\begin{align*}
F_R(\omega) &= \frac{1}{\pi} P \int_{-\infty}^{\infty} \frac{F_I(x)}{x-\omega}dx\\
F_I(\omega) &= -\frac{1}{\pi} P \int_{-\infty}^{\infty} \frac{F_R(x)}{x-\omega}dx\\
\end{align*}
こんなです.
主値積分については以下の記事を参考にしていただければ幸いです.
まず因果的というところから見ていきます.
2. 因果的
因果的というのは関数がちょうど始まりの時刻からしか影響を受けていないということです.
どういうことかというと,\(t < 0\)ではまったく0で,\(t \geq 0\)から何かしらの値をとるような関数ということです.
式の形でかくと,
\begin{equation} f(t) = \left\{ \begin{alignedat}{2} 0 & \quad (t < 0) \\ f(t) & \quad (t \geq 0) \end{alignedat} \right. \end{equation}
この性質がフーリエ変換後の複素関数である\(F(\omega)\)が上半面に極を持たないという重要な性質につながります.
3. \(F(\omega)\)の極配置について
まず追加で1つ仮定をしておきます.
\(F(\omega)\)は上半面の十分遠方で0に収束する
そもそも複素積分を考えたい状況ですので,積分の際に発散してしまうようなケースを除きます.
そこまでおおげさな仮定ではないかと思います.
さて,では以下のよくある積分路を考えます.
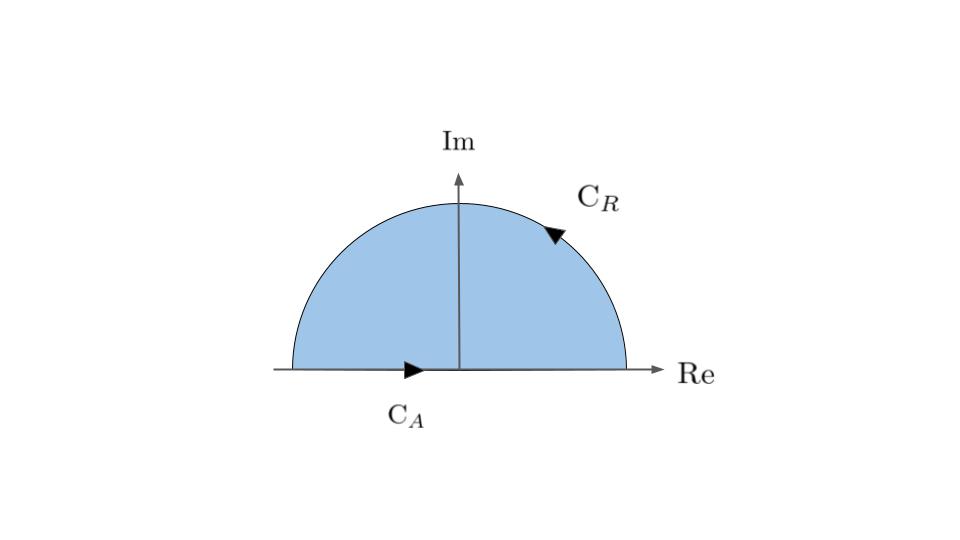
\(C_R\)は半径\(R\)の上半円弧,\(C_A\)は実軸上の\(-RからRまで\)の線分だとします.
一周する積分路は\(C = C_R + C_A\)と書くことにします.
\(F(\omega)\)は十分遠方で収束すると仮定したので,\(R \to \infty\)とすると\(C_R\)上を\(\omega = a + ib\)が動くとき,\(b > 0\)であり,\(b \to \infty\)となります.よって\(t <0\)とすると,
\begin{align*}
\frac{1}{2\pi} \int_{C_R} F(\omega) e^{-i\omega t} d\omega
&= \frac{1}{2\pi} \int_{C_R} F(\omega) e^{-ia t} e^{bt} d\omega\quad (\omega = a+ ib)\\
&\to 0
\end{align*}
となって\(C_R\)上での積分は消すことができます.
\(t < 0\)でのフーリエ変換の式を立てます.因果性より\(f(t) = 0\)であることから,
\begin{align*}
0 = f(t)
&= \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega) e^{-i\omega t} d\omega \\
&= \lim_{R\to\infty}\frac{1}{2\pi} \oint_{C} F(\omega) e^{-i\omega t} d\omega
\end{align*}
ここで,もし上半面に\(F(\omega)\)の極があったとすると,留数定理から
\[\oint_{C} F(\omega) e^{-i\omega t} d\omega \neq 0\]
よって0でなくなってしまいますから左辺と一致せずおかしいです.
よって\(F(\omega)\)は上半面に極を持たないことが分かります.
4. 積分路
ここまででフーリエ変換\(F(\omega)\)が上半面に極を持たないことがわかりましたので,上半面をカバーするような積分路をとれば,計算がしやすそうです.
求めたいKramers-Kronigの関係式は
\[\frac{F(z)}{z- \omega}\]
を積分したものです.
この被積分関数の極は,上半面においては\(z = \omega\)のみですから,主値積分のやり方通りに\(z = \omega\)を迂回するように,半径\(\epsilon\)の円の積分路をとりましょう.つまりこんな感じです.
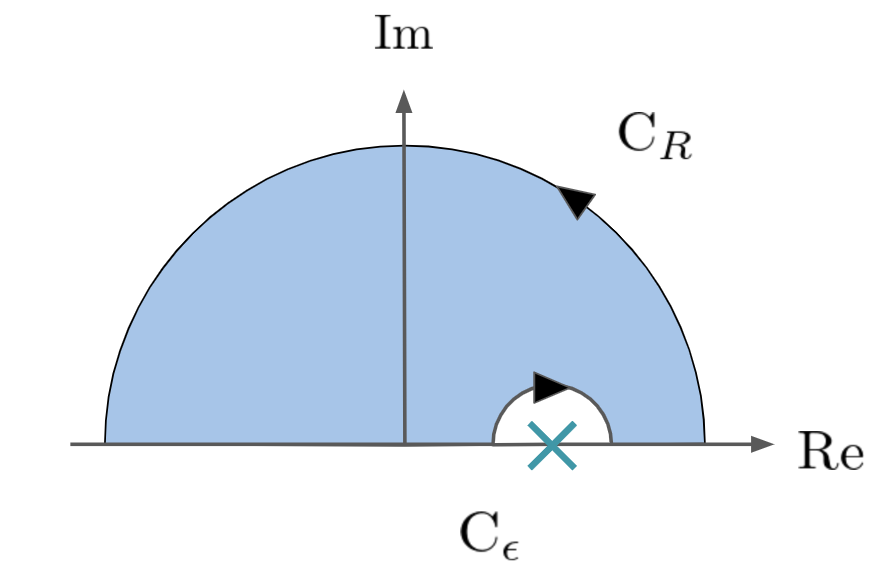
実軸上のバツ印が極\(z = \omega\)を表しています.
さてではこの積分路に沿って計算をしていきます.
5. Kramers-Kronigの関係式の導出
さきほどの積分路を3つのパートに分けます.
一周の経路を\(C\)として,
\begin{align*}
\oint_C = \underset{1つ目}{\underline{\int_{C_R}}} + \underset{2つ目}{\underline{\int_{-R}^{\omega – \epsilon} + \int_{\omega + \epsilon}^{R}}} + \underset{3つ目}{\underline{\int_{C_\epsilon}}}
\end{align*}
という感じにすると見通しがよさそうですね.
- 1つ目がいちばん外側の半径\(R\)の円弧
- 2つ目が極をスキップした実軸上の積分
- 3つ目が上半面を通って極を迂回するように設定した半径\(\epsilon\)の円弧
となっています.それではそれぞれの積分を考えていきましょう.
1つ目の積分
\[\int_{C_R} \frac{F(z)}{z – \omega} dz\]
については,\(F(\omega)\)は上半面の十分遠方で0に収束するという仮定を置いていたので,\(R \to \infty\)で\(0\)になります.
2つ目の積分
\[\left(\int_{-R}^{\omega – \epsilon} + \int_{\omega + \epsilon}^{R}\right) \frac{F(x)}{x – \omega} dx\]
についてですが,これこそ主値積分ですね.
\(\epsilon \to 0,\ R \to \infty\)とすることで,定義通り
\[\lim_{\epsilon \to 0} \lim_{R \to \infty} \left(\int_{-R}^{\omega – \epsilon} + \int_{\omega + \epsilon}^{R}\right) \frac{F(x)}{x – \omega} dx = P \int_{-\infty}^{\infty} \frac{F(x)}{x – \omega} dx \]
となります.
3つ目の積分
\[\int_{C_\epsilon} \frac{F(z)}{z – \omega} dz\]
について考えます.
\(C_\epsilon\)上では\(z = \omega + \epsilon e^{i\theta}\ (0\leq \theta \leq \pi)\)と表されます.積分路は\(C_\epsilon\)を時計回りに取っているので,
\begin{align*}
\int_{C_\epsilon} \frac{F(z)}{z – \omega} dz
&= \int_{\pi}^0 \frac{F(\omega + \epsilon e^{i\theta})}{\epsilon e^{i\theta}} \frac{dz}{d\theta} d\theta \\
&= \int_{\pi}^0 \frac{F(\omega + \epsilon e^{i\theta})}{\epsilon e^{i\theta}} i\epsilon e^{i\theta} d\theta \\
&= i\int_{\pi}^0 F(\omega + \epsilon e^{i\theta}) d\theta
\end{align*}
ここで\(\epsilon \to 0\)とするので,\(\epsilon\)が十分小さいと考えれば,
\begin{align*}
i\int_{\pi}^0 F(\omega + \epsilon e^{i\theta}) d\theta
&\simeq i\int_{\pi}^0 F(\omega) d\theta \\
&= iF(\omega) \int_{\pi}^0 d\theta \\
&= -iF(\omega) \pi
\end{align*}
となります.あらっぽい議論ですが,
\[\lim_{\epsilon \to 0}\int_{C_\epsilon} \frac{F(z)}{z – \omega} dz = -iF(\omega) \pi\]
となりました.
まとめると
積分路を思い出すと,\(F(\omega)\)自体は上半面で極がなく,実軸上の極は迂回するようにして避けたので,積分路で囲まれた領域に極はありません.
よって留数定理(この場合コーシーの積分公式ですが)より,
\[\oint_{C} \frac{F(z)}{z – \omega} dz = 0\]
です.よって先ほど3つにわけた積分たちをまとめて\(\epsilon \to 0,\ R \to \infty\)とすれば,
\[P\int_{-\infty}^{\infty} \frac{F(x)}{x – \omega}dx – i\pi F(\omega) = 0\]
となります.\(F(\omega) = F_R(\omega) + iF_I(\omega)\)を代入しましょう.
\begin{align*}
F_R(\omega) + iF_I(\omega) &= -i\frac{1}{\pi} P \int_{-\infty}^{\infty} \frac{F_R(x) + iF_I(x)}{x-\omega}dx\\
&= \frac{1}{\pi} P \int_{-\infty}^{\infty} \frac{F_I(x) -iF_R(x)}{x-\omega}dx\end{align*}
ということで実部と虚部を見比べることで,Kramers-Kronigの式
\begin{align*}
F_R(\omega) &= \frac{1}{\pi} P \int_{-\infty}^{\infty} \frac{F_I(x)}{x-\omega}dx\\
F_I(\omega) &= -\frac{1}{\pi} P \int_{-\infty}^{\infty} \frac{F_R(x)}{x-\omega}dx\\
\end{align*}
を得ます.
因果律ってかなり単純な仮定だと思いますが,そこから出発して実部と虚部を結びつけるようなKK関係が出てくるというのはふしぎです

ここまで読んでくださいましてありがとうございました

コメント