複素関数のグラフってどう描くの？【複素関数の初歩１】

「複素関数」ってすごくかっこいい響きですよね

でも同時にイメージしがたい難解な雰囲気も漂わせていますよね

僕が高校数学ではじめて\(f(x)\)に出くわしたときはなんか難しいなあと思っていました

そんな僕を助けてくれたのがグラフです

ということで複素関数をイメージするために、そのグラフを考えていきたいです

１．一変数実関数のグラフが描けるわけ

高校生のときは反抗期だったこともあり、親の顔より見た\(y=f(x)\)　

これってなんで平面に図示できるんでしょうか？

例えば\(f(x)=x^2\)を考えてみます

この関数\(f\)は、与えられた数字の二乗を返します

一般的に言うと、青い数直線上の点が赤い数直線上のどの点に移るのかっていう関係が\(f\)なんです

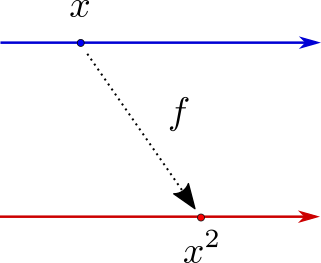
この赤い数直線を９０度回転させて、二本の数直線の\(0\)を重ねれば

おなじみの放物線のグラフになります

さて本題、なぜ放物線のグラフが描けたんでしょうか？

それは\(x\)の値を表す数直線と\(y\)の値を表す数直線の計二本を合体させたからです

一変数実関数は一次元の\(x\)と一次元の\(y\)の関係を二次元の\(xy\)平面で考えているから、平面上にグラフを描くことができるんですね

これは次元だけに注目すると「\(1+1=2\)」という式に対応しています

この「次元を足す」的な感覚が複素関数のグラフを考える上でのヒントになります

２．複素関数のグラフは何次元？

ではメインテーマである複素関数のグラフについて考えます

一般に複素関数\(f\)とは、複素数\(z\)に対し複素数\(w=f(z)\)を対応させる関係のことです

もう少し具体的に書いてみます

複素数は実部と虚部の計二つの実数を決めれば、一つに定まりますよね

なので複素関数は、複素数\(z=x+iy\)に対し複素数\(w=u+iv\)を対応させるということもできますよね

つまりこの図のように、青丸を赤丸へ移すのが\(f\)です

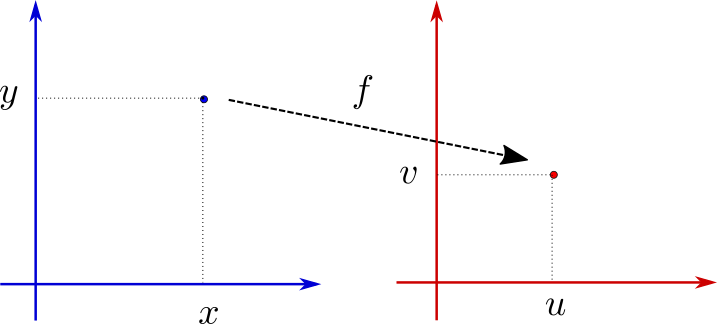
ここで、\(u\)は\((x, y)\)の実関数「\(u=u(x, y)\)」であり、\(v\)も\((x, y)\)の実関数「\(v=v(x, y)\)」であることに注意します

すると青い二次元の\(xy\)平面と赤い二次元の\(uv\)平面の対応ですから、合体させてみましょう
さきほどの「次元を足す」ことを思い出してみると・・・

４次元

になります

ぜひ皆さんのたくましい想像力で思い描いてみてください

とはいえ４次元以上となるとビジュアルに図示することは現実的ではないですね

イメージのしづらい複素関数のグラフを図示するには４次元を描く必要があるということで、断念するしかないようです

３．複素関数を「見る」方法

複素関数のグラフを図示することは断念しましたが、やっぱり複素関数をビジュアルで見たいです

そもそも一変数実関数のように「合体」させてしまったために４次元を図示する必要が出てきてしまったわけです

そこで提案なのですが

定義域の平面も値域の平面も描く

というのはいかがでしょうか、合体させずに別々に描いてみるのです

例えば　\(f(z)=e^z\)　を考えてみます

実数\(x, y\)を用いて\(z=x+iy\)と書いてみると、オイラーの公式より

$$f(z)=e^{x+iy}=e^x \cdot e^{iy}=e^x( \cos y+i \sin y)$$

というように書き直せます

さてここで定義域\(D\)を$$D= \{ z=x+iy \quad | \quad 0 \leq x \leq 1, \quad 0 \leq y \leq \frac{\pi}{2} \} $$

としてみましょう　この水色の長方形が\(D\)です

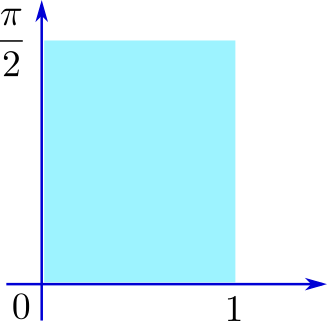
さて水色の長方形領域の点\(z\)が関数\(f\)によってどのような図形に移されるのか考えます

いきなり長方形がどう移るか考えるのはちょっと難しめなので
長方形をタテ線の集まりと見てみましょう

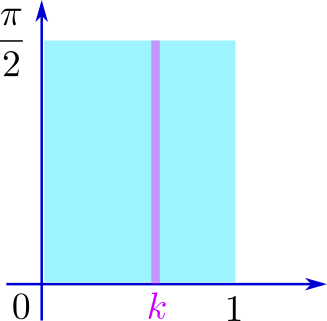
その内の一本、実部が\(k\)の複素数の集合であるパープルの線分に注目してみます

\(e^k\)が定数になっていることに注意すると、この線分上の複素数\(z\)は$$z=e^k(\cos y+i \sin y)$$

これって\(r=e^k, \theta = y\)の極形式になっていますね

今回パープルの線分の長さは\(0 \leq y \leq \frac{\pi}{2} \)ですから

半径\(e^k\)の中心角\( \frac{\pi}{2}\)の円弧になりますよね

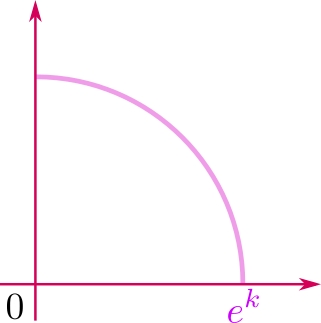
パープルの線分がくねっと曲がってパープルの円弧になったというイメージ、できますか？

これを長方形\(D\)全体で同じことをイメージします

つまり\(k\)を\(0\)から\(1\)まで動かして、パープルの線分をひとつひとつ丹念に心をこめて、くねっと曲げてパープルの円弧を作っていきます

ちょうどバウムクーヘンの層みたいに重なっていく感じです

さて\(k\)を\(0\)から\(1\)まで動かしきると、円弧は半径\(1\)から半径\(e\)まで重なって

このように値域\(f(D)\)は赤い円環の四分の一になるんですね

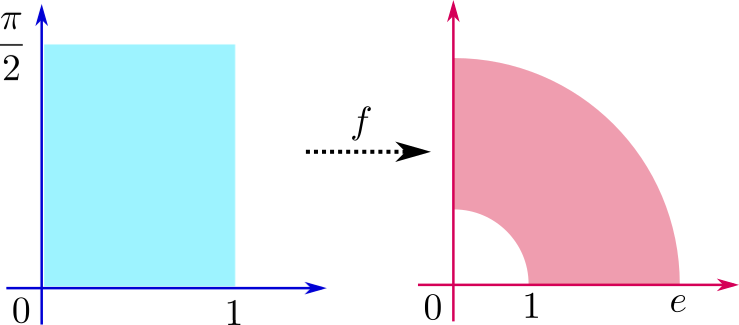
まとめると、今考えた関数\(f(z)=e^z\)は
長方形の下側を持ったまま、上側をひねって、ちょうどアコーディオンみたいにして円環の一部に変形するという対応を表しているのですね

イメージできたでしょうか

さてここで、これまで考えてきたイメージの仕方が使えるかどうか確かめるために、\(D\)を変化させると値域\(f(D)\)がどう変化するか考えてみてください

【問】\(D\)の\(x\)の条件を「\(-1 \leq x \leq 2 \)」にすると値域はどうなるでしょう？

【問】\(D\)の\(y\)の条件を「\(0 \leq y \leq 2\pi \)」にすると値域はどうなるでしょう？

【問】\(D\)の\(y\)の条件を「\(2\pi \leq y \leq 4\pi \)」にすると値域はどうなるでしょう？

ちょっとだけ一般化すると、\(m, n\)を整数として関数\(f(z)=e^z\)は領域\(D_1, D_2\)が$$D_1= \{ z=x+iy \quad |\quad r \leq x \leq R, \quad 2n\pi \leq y \leq 2(n+1)\pi \}$$ $$D_2= \{ z=x+iy \quad |\quad r \leq x \leq R, \quad 2m\pi \leq y \leq 2(m+1)\pi \}$$

をみたすとき、定義域が\(D_1\)でも\(D_２\)でも

内径\(e^r\)、外径\(e^R\)の円環に移ります

こんな感じです　\(r=0, R=1\)としました

上下に無限個ある水色の長方形一つずつ全部が、同じ赤い円環に移ります

このような感じで定義域と値域を別々に描いてあげると複素関数がどのような対応を表しているのか
見えてくるのではないでしょうか

４．まとめ

複素関数をビジュアル化するためには、

今回扱った\(f(z)=e^z\)を見る時は
定義域内で実部を固定することで定義域をタテ線にグループ分けし、そのタテ線一本一本の動きを観察することで値域を確認しました

これはあくまで一提案ですが、複素関数のイメージに役立つのではないかなと思います