コーシーの主値積分は複素積分のやり方の1つです.
ざっくり主値積分の計算方法をいうと,
極を半径\(\epsilon\)の円を使って迂回し,最終的に\(\epsilon\)を小さくして計算する
というものです.
名前はかっこいいですが,計算上は基本これだけです.
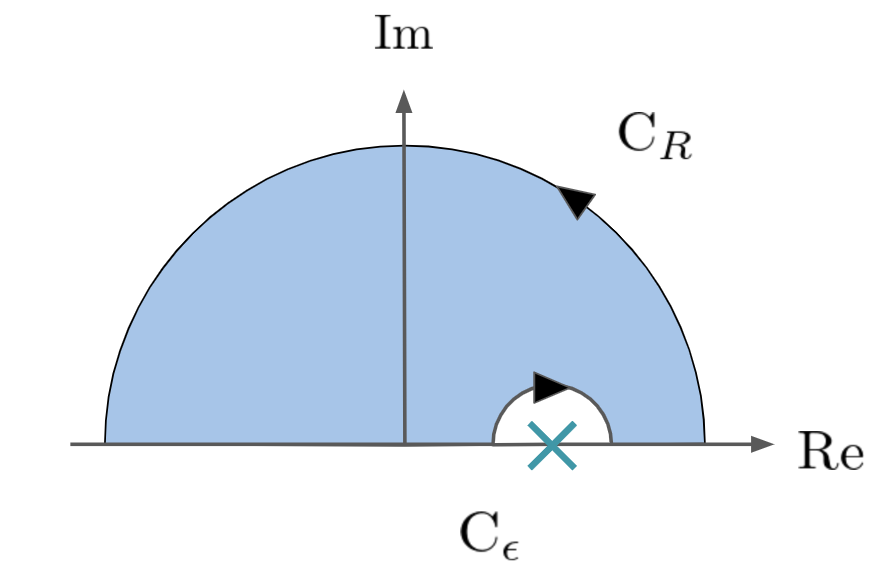
極からの距離を\(\epsilon\)に固定して極限をとるので,任意の近づき方で極周辺の極限を調べているわけではないです.なので特別に主値積分と呼ばれています.
1. コーシーの主値積分
まずはじめにどんな状況でつかわれるものなのか書きます.
コーシーの主値積分
実軸上に極\(x = \alpha\)を持つ関数\(f\)の積分を考える.このとき,極から\(\epsilon\)離れたところまででの積分を求め,\(\epsilon \to 0\)とした極限値をコーシーの主値積分といい,以下のように積分記号の前に\(P\)をつけて表す.
\[P \int_{-\infty}^{\infty} f(x) dx = \lim_{\epsilon \to 0} \int_{-\infty}^{\alpha – \epsilon} f(x) dx + \int_{\alpha + \epsilon}^\infty f(x) dx\]
極があってそのまま積分できないときに,積分できませんでしたと報告して終わってしまうのも味気ないです.
苦肉の策として,極周りの\(\epsilon\)幅を狭めるという特殊な極限の取り方の1つではありますが,一応何かしら値を求めましたっていうのが主値積分だと思っています.
うれしいことは,\(\epsilon\)幅のことだけしか考えていないので,計算がしやすいことですね.
注意を払うべきことは,あくまで”主値”積分であって,通常の積分ではないことです.
そもそも極限というのは任意の経路を考えて収束するか見なきゃいけないものなのに,主値積分は\(\epsilon\)幅のことしか考えていません.
2. デルタ関数と主値積分
例えばこんな公式があります.
\(\delta > 0\)を微小な正数とする.上半面で正則な関数に対して,
\[\frac{1}{x – i \delta} = P\frac{1}{x} + i \pi\delta(x)\]
紛らわしい書き方ですが左辺の\(\delta\)はただのとても小さな正数です.
一方で右辺の\(\delta(x)\)はデルタ関数です.なのでこの公式は積分されることを前提としています.
ノリとしては,左辺の関数の\(z = i\delta\)という原点直上にある極による振る舞いが,実軸上の主値積分と,虚数成分としてのデルタ関数に分離できるよって感じです.
では証明してみます.
上半面で正則な関数\(f\)をとって実軸上での積分を考えていきましょう.
左辺について
積分路を次のようにとってみます.
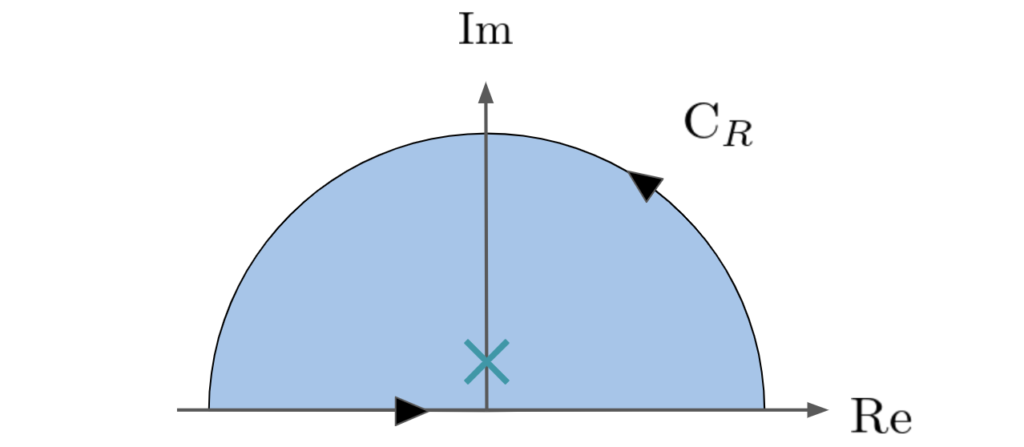
極は虚軸上の\(z = i\delta\)です.
積分路を\(C_1 = C_R + [-R, R]\)とします.\(C_R\)は半径\(R\)の上半円弧として設定しました.
まず留数定理を使うと,
\[\oint_{C_1} \frac{f(z)}{z – i\delta} dz = 2\pi i f(i\delta) \to 2\pi i f(0)\ (\delta \to 0)\]
となります.よって\(C_1 = C_R + [-R, R]\)を分けておくと,\(R \to \infty,\ \delta \to 0\)のとき,
\[\lim_{R \to \infty}\lim_{\delta \to 0}\int_{-R}^R \frac{f(x)}{x – i\delta} dx + \lim_{R \to \infty}\lim_{\delta \to 0}\int_{C_R} \frac{f(z)}{z – i\delta} dz = 2\pi i f(0) \]
よって
\[\lim_{\delta \to 0}\int_{-\infty}^\infty \frac{f(x)}{x – i\delta} dx = -\lim_{R \to \infty}\int_{C_R} \frac{f(z)}{z} dz + 2\pi i f(0) \]
となります.
右辺について
右辺については
\[\frac{f(z)}{z}\]
という関数の積分を考えて導いていきます.
この関数の極である原点を迂回するような積分路をとってみます.
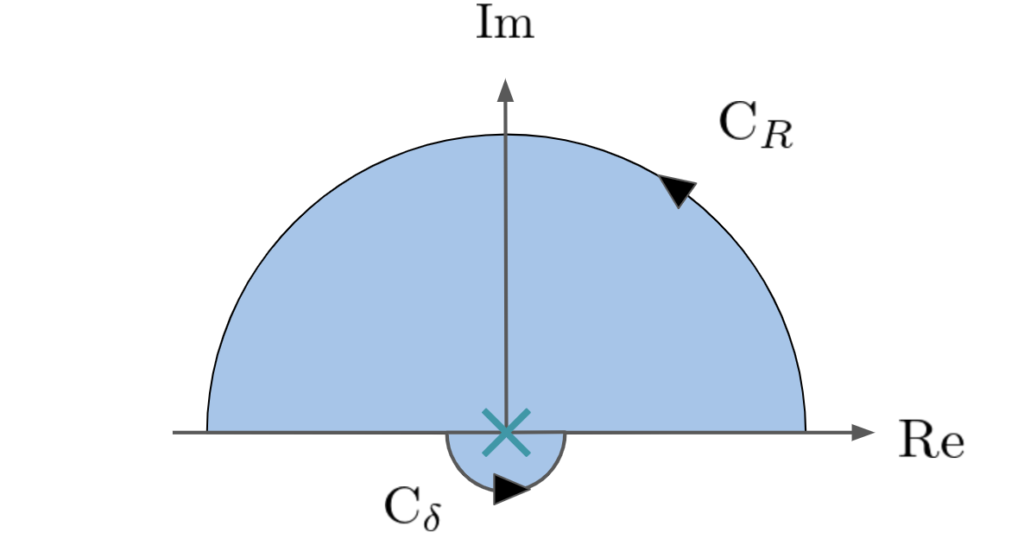
\(C_\delta\)は半径が\(\delta\)の下半円弧です.
この積分路を\(C_2 = C_R + [-R, -\delta] + C_\delta + [\delta, R]\)と名付けることにします.
最終的には\(\delta \to 0\)とするので,左辺で考えていた積分路と一致することになります.
まずは留数定理から,極は\(z=0\)のみですから,
\[\oint_{C_2} \frac{f(z)}{z} dz = 2\pi i f(0) \]
さて,ではまた積分路の各パーツごとに積分値を確認しましょう.
まず\(C_\delta\)について,
\begin{align*}
\int_{C_\delta} \frac{f(z)}{z} dz
&= \int_{-\pi}^0 \frac{f(\delta e^{i\theta})}{\delta e^{i\theta}} i \delta e^{i\theta} d\theta \\
&= i\int_{-\pi}^0 f(\delta e^{i\theta}) d\theta \\
&\to i\int_{-\pi}^0 f(0) d\theta\quad (\delta \to 0) \\
&= i \pi f(0) \\
&= i \pi \int_{-\infty}^\infty f(x) \delta (x) dx \\
\end{align*}
となります.デルタ関数が出てきました.
続いて実軸上の区間に注目します.こちらからは主値積分がでてきます.
\begin{align*}
\ \left(\int_{-R}^{-\delta} + \int_{\delta}^{R} \right) \frac{f(x)}{x} dx
&\to P \int_{-\infty}^{\infty} \frac{f(x)}{x} dx \quad (\delta \to 0,\ R \to \infty)
\end{align*}
\(C_R\)での積分は
\[\lim_{R \to \infty} \int_{C_R} \frac{f(z)}{z} dz\]
となるだけですから,まとめると\(\delta \to 0,\ R \to \infty\)
\[ P \int_{-\infty}^{\infty} \frac{f(x)}{x} dx +i \pi \int_{-\infty}^\infty f(x) \delta (x) dx + \lim_{R \to \infty} \int_{C_R} \frac{f(z)}{z} dz = \oint_{C_2} \frac{f(z)}{z} dz \]
ですから,
\[ P \int_{-\infty}^{\infty} \frac{f(x)}{x} dx +i \pi \int_{-\infty}^\infty f(x) \delta (x) dx = -\lim_{R \to \infty} \int_{C_R} \frac{f(z)}{z} dz + 2 \pi i f(0) \]
まとめると
\[\lim_{\delta \to 0}\int_{-\infty}^\infty \frac{f(x)}{x – i\delta} dx = P \int_{-\infty}^{\infty} \frac{f(x)}{x} dx +i \pi \int_{-\infty}^\infty f(x) \delta (x) dx \]
となります.よって微小な正数\(\delta\)を考えたときには,この式における\(f\)に対する操作を作用素として等しいととらえて,
\[\frac{1}{x – i \delta} = P\frac{1}{x} + i \pi\delta(x)\]
という公式を得ることができます.

最後までお読みいただきありがとうございました

コメント