高校数学で
\(y=2x+1 (1 \leq x < 2)\) について \(y\) の最大値および最小値を求めよ
最小値 \(3\) (\(x=1\))/最大値なし…(答)
こういう問題をはじめて見たときはなんか違和感を感じませんでしたか?
僕は「最大値なし」と言われてもなんか腑に落ちませんでした
たしかに \(x\) は \(2\) をとれないので最大値を \(y=5\) とすることは絶対だめです
だからといって \(\alpha\) という数が存在して \(y=2 \alpha +1\) が最大値だと仮定しても
$$\beta =\frac{\alpha +2}{2}$$
は \(\alpha<\beta<2\) という不等式を満たすので \(y=2 \beta +1\) の方が大きいこととなり矛盾してしまいます
やっぱり最大値はないんです
でもなんかこの「\(y=5\)」に名前くらいつけてあげてもいいんじゃないかと思ってました
大学に入ってからこれに名前が付いていることを知りました
それが「上限」です
ということで最大値と上限の違いを書いてみました
1.上限の定義と最大値との違い
上限について書いていきますが、今考えているのは実数 \(\mathbb{R}\) であることを常に頭の片隅に置いておいていただけると幸いです
- \(A\)を\(\mathbb{R}\)の空でない部分集合としたとき、もしある \(b \in \mathbb{R}\) が存在してすべての \(x \in A\) に対し \(x \leq b\) を満たすならば、\(A\)は上に有界であるという
- また上記の条件をみたす \(b\) を\(A\)の上界という
- \(A\)の上界のうち、最小のものを\(A\)の上限といい、\(\sup A\)と表す
一気に「上に有界」、「上界」、「上限」の定義を書いたのでゆっくり読んでいただけると幸いです
要するに黄色マーカーの条件をみたす \(b\) の最小値が \(\sup A\) です
文章を数直線を使って図にしてみると
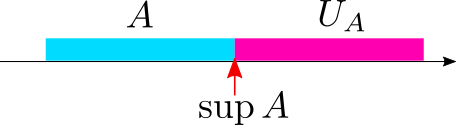
こんなイメージです \(U_A\) は \(A\) の上界全体の集合、つまり定義の中で登場した \(b\) 全体の集合ですね
さて最大値の定義も見てみましょう
\(A\)を\(\mathbb{R}\)の空でない部分集合としたとき、もしある \(b \in A\) が存在してすべての \(x \in A\) に対し \(x \leq b\) を満たすならば、この \(b\) を \(A\) の最大値といい、 \(b=\max A\) と表す
ここまで読んでみて \(\sup A\) と \(\max A\) の違いにお気づきでしょうか
ヒントは、黄色マーカーに注目することです
正解は…
「上限では \(b \in \mathbb{R}\) だが最大値では \(b \in A\)となっている」 でした
つまり
\(\max A\) は必ず \(A\) に属するが \(\sup A\) は \(A\) に属してても属してなくてもよい
というのが大きな違いです
ただし \(\sup A \in \mathbb{R}\) は絶対です 当たり前なんですけどね
ちょっと一般化すると全体集合を \(U\) として \(A \subset U\) に対し \(\sup A \in U\) です
全体集合を \(U\) として \(A \subset U\) とする
\(\sup A\) は \(A\) に属してても属してなくてもよいが、 \(\sup A \in U\) は絶対
なんでこんなこと言うかというと上限がいつも存在するとは限らないからです
その具体例は上限の性質を確認した後で見たいと思います
2.上限の性質
上限を特徴づける性質はこの2つです \(\mathbb{R}\) の部分集合 \(A\) をとって
- すべての \(x \in A\) に対し \(x \leq \sup A\)
- \(c < \sup A\) ならば \(c < x\) を満たす \(x \in A\) が存在する
1.の条件は \(\sup A\) が上界の一つであることを言っています
これは単なる上界の定義ですから分かりやすいですね
2.の条件は \(\sup A\) よりも小さい上界は存在しないことを言っています
こっちはちょっとわかりづらいですね、もう少しかみ砕くと
『上限よりも小さい実数をとると、その実数より大きい \(A\) の元が存在する』ってことです
この「その実数より大きい \(A\) の元が存在する」というのが上界の定義の否定になっていることに注目すると理解しやすいと思います
つまり『上限より小さい実数は上界ではない』ってことですね
よってある数が上限であることを示すには、この2つの条件を満たすことを示すのが定石です
【例題】 \(A=\{1-\frac{1}{n}\: |\: n \in \mathbb{N} \} \) のとき \(\sup A=1\) を示せ
まず1.の条件を満たしていることを確認する
すべての \(n \in \mathbb{N}\) に対して \(1-\frac{1}{n} < 1\)
つぎに2.の条件を満たしていることを確認する
\(c < 1\) を満たす \(c\) に対して \(n_0 > \frac{1}{1-c}\) を満たす \(n_0 \in \mathbb{N}\) が存在するので \(1-c >0\) に注意して式変形すると
$$n_0>\frac{1}{1-c}$$ $$\frac{1}{n_0} < 1-c$$ $$c < 1-\frac{1}{n_0}$$
よって \(x=1-\frac{1}{n_0}\) とすれば \(c < x\) であり \(x \in A\) を満たす ■
2.の条件を調べるときや \(\varepsilon – \delta\)論法など
存在を示すときには欲しい条件を変形して天下り的に導くとうまくいくことがあります
つまりまずは欲しい条件である \(c < 1-\frac{1}{n}\) を書き出して、これを変形して \(n > \frac{1}{1-c}\) を得て、あたかも \(n > \frac{1}{1-c}\) という条件を閃いたみたいに解答を書くんですね
逆に問題文で上限が与えられていれば、この2つの性質を使って解いていくことになります
- 上限は上界の一つである
\(\iff \) すべての \(x \in A\) に対し \(x \leq \sup A\) - 上限より小さい実数は上界ではない
\(\iff \) \(c < \sup A\) ならば \(c < x\) を満たす \(x \in A\) が存在する
3.上限がない集合ってあるの?
僕が感じていた高校数学で感じていた「最大値なし」というモヤモヤを上限が解消してくれました
しかし上限がいつでもあるかというと、そうでもないです
具体例を挙げます
【ex】有理数全体の集合 \(\mathbb{Q}\) の部分集合 \(A=\{a \: | \: a^2 < 2\} \) は \(\mathbb{Q}\) において上限をもたない
上限は上界の中で最も小さい数ですから、 \(A\) 上界全体の集合を \(U_A\) とおくと$$U_A= \{ a \: | \: 2 \leq a^2\}$$
となりますので \(U_A\) の最小元は \(\sqrt{2}\) ! \(\sup A\) は \(\sqrt{2}\) !
としたくなるかもしれませんがダメですね
というのもそもそも \(\sqrt{2}\) が今の全体集合 \(\mathbb{Q}\) の元でないからです
全体集合に属していない元が議論に割り込んできては全体集合をわざわざ制限した意味がありませんよね
もし \(A\) が \(\mathbb{R}\) の部分集合だとするならば上限は存在して \(\sup A=\sqrt{2}\) です
ということで至極当然のことではあるのですが \(\sup\) を考えるときも全体集合がどの範囲なのかを忘れることがないようにしたいですね
4.まとめ
\(\max A\) は \(A\) の中にあり、\(\sup A\) は \(A\) の中でも外でもどちらにあってもいい
というのが大きな違いでした
最大値と上限は似ていますがしっかり違う部分もありましたね
今回は全く触れませんでしたが最小値と下限の違いもこれと同じです

最後まで読んでくださいましてありがとうございました


コメント